Пол Дірак, «Scientific American», травень 1963 р.
У цій статті я хотів би обговорити розвиток загальної фізичної теорії: як вона розвивалася в минулому і якого можна очікувати її розвитку в майбутньому. Можна розглядати цей постійний розвиток як процес еволюції, процес, що триває вже кілька століть.
Перший головний крок у цьому процесі еволюції зробив Ньютон. До Ньютона люди дивилися на світ як на по суті двовимірний – два виміри, у яких можна ходити, – а вимір вгору-вниз здавався чимось істотно інакшим. Ньютон показав, що можна дивитися на напрямок вгору-вниз як на симетричний з двома іншими напрямками, вводячи сили тяжіння і показуючи, як вони займають своє місце у фізичній теорії. Можна сказати, що Ньютон дозволив нам перейти від картини з двовимірною симетрією до картини з тривимірною.
Айзек Ньютон (1642–1727), завдяки своєму законові тяжіння, змінив фізикову картину природи з такої, що з двовимірною симетрією, на таку, що з тривимірною. Цей його малюнок виконав 1760 року Джеймз Макардел з картини Іноха Секмена.
Альберт Айнштайн (1879–1955) своєю спеціальною теорією відносності змінив фізикову картину з тривимірною симетрією на таку, що з чотиривимірною. Ця фотографія його, його дружини та їхньої дочки Марго зроблена 1929 року.
Нільс Бор (1885–1962) запропонував ідею, що електрон рухається навколо ядра чітко визначеними орбітами. Ця фотографія зроблена 1922-го, через дев'ять років після публікації його статті.
Макс Планк (1858–1947) запропонував ідею, що електромагнетне проміння складається з квантів, або частинок. Ця фотографія зроблена 1913-го, через 13 років після публікації його статті.
Люї де Бройль (1892–) висунув ідею, що частинки пов'язані з хвилями. Ця фотографія зроблена 1929-го, через п'ять років після появи його статті.
Ервін Шредінґер (1887–1961) винайшов хвильове рівняння, розширивши ідею Де Бройля про те, що хвилі пов’язані з частинками до електронів, що рухаються навколо ядра. Ця фотографія зроблена 1929-го, через чотири роки після того, як він опублікував своє друге рівняння.
Вернер Гайзенберґ (1901–) запровадив матричну механіку, що, як і теорія Шредінґера, пояснювала рухи електрона. Ця фотографія зроблена 1929 року.
[Усі зображення див. в оригінальному тексті].
Айнштайн зробив ще один крок у тому ж напрямку, показавши, як можна перейти від картини з тривимірною симетрією до картини з чотиривимірною. Айнштайн ввів час і показав, яку він відіграє роль, що багато в чому симетрична з трьома просторовими вимірами. Однак ця симетрія не зовсім бездоганна. В межах картини Айнштайна, це веде до того, щоб думати про світ з чотиривимірного погляду, але ці чотири виміри не цілком симетричні. У чотиривимірній картині є деякі напрями, що відрізняються від інших: напрями, які називаються нульовими (ізотропними), вздовж яких може рухатися промінь світла; отже, чотиривимірна картина не повністю симетрична. Проте існує велика кількість симетрії серед чотирьох вимірів. Єдиний недолік симетрії, коли йдеться про рівняння фізики, полягає в появі знака мінус у рівняннях щодо часового виміру, якщо порівняти з трьома просторовими вимірами [див. верхнє рівняння на ВСТАВЦІ].
ВСТАВКА
ds2 = c2dt2 – dx2 – dy2 – dz2
ЧОТИРИВИМІРНА СИМЕТРІЯ, запроваджена спеціальною теорією відносності, не зовсім досконала. Це рівняння – вираз для інваріантної відстані в чотиривимірному просторочасі. Символ s – інваріантна відстань; c – швидкість світла; t – час; x, y та z – три просторові виміри. d – диференціали. Брак повної симетрії полягає в тому, що внесок від часового напрямку (c2dt2) не має такого самого знака, як внески від трьох просторових напрямків (– dx2, – dy2 і – dz2).
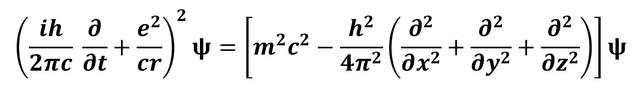
ПЕРШЕ ХВИЛЬОВЕ РІВНЯННЯ ШРЕДІНҐЕРА не відповідало експериментальним результатам, бо воно не враховувало спін електрона, що на той час не був відомий. Рівняння – узагальнення рівняння де Бройля для руху вільного електрона. Символ e позначає заряд на електроні; i – квадратний корінь з мінус один; h – константа Планка; r – відстань від ядра; ψ – хвильова функція Шредінґера; m – маса електрона. Символи, схожі на повернуті назад шістки – часткові похідні.
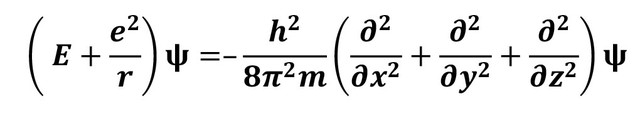
ДРУГЕ ХВИЛЬОВЕ РІВНЯННЯ ШРЕДІНҐЕРА – наближення до початкового рівняння, яке не враховує уточнення, що вимагає теорія відносності.
Отже, ми маємо розвиток від тривимірної картини світу до чотиривимірної. Читач, мабуть, не буде задоволений такою ситуацією, бо світ все ще здається тривимірним для його свідомості. Як можна внести цей феномен у чотиривимірну картину, якої Айнштайн вимагає від фізика?
Те, що видається нашій свідомості, – насправді тривимірний переріз чотиривимірної картини. Ми повинні взяти тривимірний переріз, щоб дати нам те, що здається нашій свідомості в один час; пізніше ми матимемо інший тривимірний переріз. Завдання фізика здебільшого складається з пов’язування подій в одному з цих перерізів з подіями в іншому перерізі, що стосуються пізнішого часу. Отже, картина з чотиривимірною симетрією не дає нам усієї ситуації. Це стає особливо важливим, якщо взяти до уваги наслідки, спричинені квантовою теорією. Квантова теорія навчила нас, що ми повинні брати до уваги процес спостереження, і спостереження зазвичай вимагають від нас введення тривимірних перерізів чотиривимірної картини Всесвіту.
Спеціальна теорія відносності, яку ввів Айнштайн, вимагає від нас виражати всі закони фізики у формі, що відображає чотиривимірну симетрію. Але коли ми використовуємо ці закони для отримання результатів спостережень, то маємо внести щось додаткове до чотиривимірної симетрії, а саме тривимірні перерізи, які описують наше усвідомлення Всесвіту на певний час.
Айнштайн зробив ще один щонайважливіший внесок у розвиток нашої фізичної картини: він висунув загальну теорію відносності, що вимагає від нас покладати, що простір фізики викривлений. До цього фізики завжди працювали з плоским простором, тривимірним плоским простором Ньютона, який потім був розширений до чотиривимірного плоского простору спеціальної теорії відносності. Загальна теорія відносності зробила справді важливий внесок у розвиток нашої фізичної картини, вимагаючи від нас переходу до викривленого простору. Загальні вимоги цієї теорії означають, що всі закони фізики можуть бути сформульовані у викривленому чотиривимірному просторі, і вони демонструють симетрію серед цих чотирьох вимірів. Але знову ж таки, коли ми хочемо внести спостереження, як мусимо, якщо ми дивимося на речі з позиції квантової теорії, то маємо покликатися на переріз цього чотиривимірного простору. За викривленого чотиривимірного простору будь-який переріз, який робимо в ньому, також має бути викривленим, бо загалом ми не можемо надати сенсу плоскому перерізові у викривленому просторі. Це приводить нас до картини, коли нам доводиться робити викривлені тривимірні перерізи у викривленому чотиривимірному просторі та обговорювати спостереження в цих перерізах.
Протягом останніх кількох років люди намагалися застосувати квантові ідеї як до гравітації, так і до інших явищ фізики, і це привело до досить несподіваного розвитку, а саме: коли поглянути на теорію гравітації з позиції перерізів, можна виявити, що існують певні ступені вільності, яких вилучають із теорії. Гравітаційне поле – це тензорне поле з 10 компонентами. Виявляється, що шість компонентів достатні для опису всього, що має фізичне значення, а інші чотири можуть бути вилучені з рівнянь. Однак не можна вибрати шість важливих компонентів із повного набору 10 хоч би яким способом, який би не руйнував чотиривимірну симетрію. Отже, якщо наполягати на збереженні чотиривимірної симетрії в рівняннях, то не можна пристосувати теорію гравітації до обговорення вимірювань так, як вимагає квантова теорія, не бувши змушеним до складнішого опису, ніж це необхідно у фізичній ситуації. Цей результат змусив мене засумніватися, якою мірою фундаментальна чотиривимірна вимога у фізиці. Кілька десятиліть тому здавалося цілком певним, що потрібно виразити всю фізику в чотиривимірній формі. Але тепер здається, що чотиривимірна симетрія не має такого виняткового значення, бо опис природи іноді спрощується, коли від неї відійти.
Тепер я хотів би перейти до розвитку, якого досягла квантова теорія. Квантова теорія – це обговорення дуже дрібних речей, і вона стала основним предметом фізики за останні 60 років. У цей період фізики накопичували досить багато експериментальної інформації і розробляли теорію, яка їй відповідала, і це поєднання теорії та експерименту привело до важливого розвитку у фізиковій картині світу.
Вперше квант з’явився, коли Планк відкрив необхідність припустити, що енергія електромагнетних хвиль може існувати лише в кратних числах певної одиниці фізичної величини, залежачи від частоти хвиль, щоб пояснити закон випромінювання абсолютно чорного тіла. Тоді Айнштайн відкрив ту саму одиницю енергії, що виникає у фотоефекті. У тій ранній роботі над квантовою теорією просто потрібно було прийняти одиницю енергії, без змоги долучити її до фізичної картини.
Першою новою картиною, що з’явилася, була Борова картина атома. Це була картина, коли ми мали електрони, які рухалися певними чітко визначеними орбітами і час від часу робили стрибок з однієї орбіти на іншу. Ми не уявляли, як відбувався стрибок. Нам просто довелося прийняти це як певний розрив. Борова картина атома працювала лише для особливих прикладів, по суті, коли існував лише один електрон, що було важливим для розглянутої проблеми. Отже, картина була неповна та примітивна.
Великий прогрес у квантовій теорії відбувся 1925 р., з відкриттям квантової механіки. Цей прогрес обумовили незалежно двоє людей, спочатку Гайзенберґ та невдовзі Шредінґер, підійшовши з різних боків. Гайзенберґ працював, тримаючись близько до експериментальних доказів щодо спектрів, які накопичувались у той час, і він з'ясував, як експериментальну інформацію можна вкласти в схему, тепер відому як матрична механіка. Всі експериментальні дані спектроскопії чудово вписалися в схему матричної механіки, і це привело до зовсім інакшої картини атомного світу. Шредінґер працював з «математичнішого» боку, намагаючись знайти красиву теорію опису атомних подій, і йому допомогли ідеї де Бройля про хвилі, пов'язані з частинками. Він зміг розширити ідеї де Бройля і отримати дуже красиве рівняння, відоме як Шредінґерове хвильове рівняння, для опису атомних процесів. Шредінґер прийшов до цього рівняння завдяки чистому мисленню, шукаючи гарного узагальнення ідей де Бройля, а не тримаючись близько до експериментального розвитку предмета так, як це робив Гайзенберґ.
Я можу розповісти вам історію, яку чув від Шредінґера, про те, що, коли йому вперше спала ідея щодо цього рівняння, він негайно застосував її до поведінки електрона в атомі водню, а потім отримав результати, які не узгоджувалися з експериментом. Розбіжності виникли, бо на той момент не було відомо, що електрон має спін. Це, звісно, стало великим розчаруванням для Шредінґера, і змусило його полишити роботу на кілька місяців. Тоді він зауважив, що якщо застосовувати теорію приблизніше, не беручи до уваги уточнень, які вимагає теорія відносності, то з цим грубим наближенням його робота узгоджувалася зі спостереженням. Він опублікував свою першу роботу лише з цим грубим наближенням, і так Шредінґерове хвильове рівняння було представлене світові. Згодом, звісно, коли люди з’ясували, як правильно враховувати спін електрона, невідповідність між результатами застосування Шредінґерового релятивістського рівняння та експериментами була повністю усунена.
Думаю, що мораль цієї історії в тому, що важливіше мати красу у своїх рівняннях, ніж допасовувати їх до експерименту. Якби Шредінґер був упевненіший у своїй роботі, то міг би опублікувати її кількома місяцями раніше, і міг би опублікувати точніше рівняння. Тепер це рівняння відоме як рівняння Кляйна – Ґордона, хоча його насправді знайшов Шредінґер, і насправді знайшов ще до того, як знайшов нерелятивістський підхід до атома водню. Видається, що якщо хтось працює, виходячи з того, щоб вписати красу в свої рівняння, і якщо в нього є справді глибоке розуміння, то він перебуває на твердому шляху прогресу. Якщо між результатами своєї роботи та експерименту немає повного узгодження, не слід дозволяти собі занадто знеохочуватися, бо ці розбіжності цілком можуть бути пов’язані з незначними особливостями, не врахованих належним чином, які будуть прояснені з подальшим розробленням теорії.
Так була відкрита квантова механіка. Це привело до кардинальної зміни у фізиковій картині світу, мабуть, найбільших, що досі сталися. Ця зміна походить від нашої необхідності відмовитися від детерміністичної картини, яку ми завжди сприймали як належну. Це привело нас до теорії, що не передбачає з певністю, що має відбутися в майбутньому, але дає нам інформацію лише про ймовірність настання різних подій. Ця відмова від визначеності була дуже дискусійною темою, і деяким людям це зовсім не подобається. Це ніколи не подобалося, зокрема, Айнштайнові.
Хоча Айнштайн був один із тих, хто зробив великий внесок у розвиток квантової механіки, він, втім, завжди був неприхильний до тієї форми, у яку перетворилася квантова механіка за його життя і яку вона все ще зберігає.
Неприхильність деяких людей до відмови від детерміністичної картини можна сконцентрувати в часто обговорюваній статті Айнштайна, Подольського та Розена, що стосується труднощів, які виникають у формуванні послідовної картини, що досі дають результати згідно з правилами квантової механіки. Правила квантової механіки цілком визначені. Люди знають, як порахувати результати і як порівняти результати своїх обчислень з експериментом. Усе формально узгоджується. Це працює так добре, що ніхто не може дозволити собі не погодитися з цим. Але все-таки картина, яку ми створюємо за цим формалізмом, – предмет суперечок.
Я хотів би порадити надто не хвилюватися з приводу цієї суперечки. Я дуже чітко відчуваю, що етап, якого досягла фізика на сьогодні, ще не завершальний. Це лише один етап еволюції нашої картини природи, і нам слід сподіватися, що цей процес еволюції триватиме і в майбутньому, як у майбутньому триватиме біологічна еволюція. Сучасний етап фізичної теорії – це лише сходинка до кращих етапів, які ми матимемо в майбутньому. Можна бути цілком впевненим, що будуть кращі етапи просто тому, що є труднощі, які виникають у фізиці сьогодні.
Тепер я хотів би трохи зупинитися на труднощах у фізиці сьогодення. Читач, не експерт у цій темі, може зрозуміти, що через усі ці труднощі фізична теорія перебуває в досить поганому стані і що квантова теорія не надто добра. Я хотів би виправити це враження, сказавши, що квантова теорія – вкрай добра теорія. Вона чудово узгоджується зі спостереженням широкого кола явищ. Немає сумнівів, що це добра теорія, і єдина причина, чому фізики так багато говорять про труднощі в ній, полягає в тому, що саме такі труднощі і є цікаві. Успіхи теорії сприймаються як належне. Ніхто нікуди не дістанеться, просто розглядаючи успіхи знову і знову, тоді як, обговорюючи труднощі, люди можуть сподіватися на певний прогрес.
Труднощі у квантовій теорії є двох видів. Я б міг назвати їх труднощами 1 класу та 2 класу. Труднощі 1 класу – це труднощі, про які я вже згадував: Як можна скласти послідовну картину за правилами сучасної квантової теорії? Ці труднощі 1 класу насправді не хвилюють фізика. Якщо фізик знає, як розрахувати результати та порівняти їх з експериментом, він цілком задоволений, якщо результати узгоджуються з його експериментами, і це все, що йому потрібно. Лише філософа, який бажає мати задовільний опис природи, турбують труднощі 1 класу.
На додаток до труднощів 1 класу існують труднощі 2 класу, які випливають з того, що сучасні закони квантової теорії не завжди адекватні для отримання будь-яких результатів. Якщо просувати закони до екстремальних умов – до явищ з дуже високими енергіями або дуже малими відстанями, – іноді отримуються результати, які неоднозначні або насправді взагалі без сенсу. Тоді стає очевидно, що досягнуто меж застосування теорії і що необхідний подальший розвиток. Труднощі 2 класу важливі навіть для фізика, бо вони накладають обмеження на те, якою мірою він може використовувати правила квантової теорії, щоб отримувати результати, порівнянні з експериментом.
Я хотів би сказати трохи більше про труднощі 1 класу. Вважаю, що ними не слід надто перейматися, бо це труднощі, які стосуються сучасного етапу розвитку нашої фізичної картини і майже напевно зміняться з подальшим розвитком. Думаю, є одна сильна підстава, чому можна бути цілком упевненим, що ці труднощі зміняться. У природі існують деякі фундаментальні константи: заряд електрона (e), Планкова константа, поділена на 2π (ħ) і швидкість світла (c). З цих фундаментальних констант можна побудувати число, яке не має розмірності: число ħc/e2. Експериментально встановлено, що це число має значення 137 або дуже близько до 137. Тепер, невідома причина, чому воно має таке значення, а не якесь інакше. Різні люди висували ідеї з цього приводу, але визнаної теорії немає. І все-таки можна бути досить упевненим, що колись фізики розв’яжуть цю проблему і пояснять, чому це число має таке значення. У майбутньому буде фізика, яка працюватиме, коли ħc/e2 матиме значення 137, і не працюватиме – коли якесь інакше.
Звісно, у фізиці майбутнього три величини, ħ, e і c, не можуть всі бути фундаментальними. Лише дві з них можуть бути фундаментальними, а третя має бути похідною від них. Майже напевно, що c буде одна з двох фундаментальних. Швидкість світла, c, така важлива для чотиривимірної картини, і вона відіграє таку фундаментальну роль у спеціальній теорії відносності, зв’язуючи наші одиниці простору та часу, що вона має бути фундаментальною. Тоді ми стикаємося з тим, що з двох величин ħ та e одна буде фундаментальна, а одна – похідна. Якщо ħ – фундаментальна, e доведеться пояснювати якимось чином через квадратний корінь ħ, і видається наймалоймовірнішим, що якась фундаментальна теорія може подати e через квадратний корінь, бо квадратні корені не трапляються в основних рівняннях. Набагато ймовірніше, що e буде фундаментальною величиною, і що ħ буде пояснена через c2. Тоді в основних рівняннях не буде квадратного кореня. Думаю, у припущення, що у фізичній картині, яку ми матимемо на якомусь майбутньому етапі, e і c будуть фундаментальними величинами, а ħ – похідною, надійний ґрунт.
Якщо ħ – похідна величина, а не фундаментальна, весь наш набір уявлень про невизначеність зміниться: ħ – це фундаментальна величина, яка виникає у співвідношеннях невизначеностей Гайзенберґа, з'єднуючи величину невизначеності в положенні та в імпульсі. Це співвідношення невизначеностей не може грати фундаментальної ролі в теорії, у якій саме ħ не фундаментальна величина. Думаю, можна впевнено припустити, що співвідношення невизначеностей не залишаться в їхньому теперішньому вигляді у фізиці майбутнього.
Звісно, повернення до детермінізму класичної фізичної теорії не буде. Еволюція не йде назад. Має йти вперед. Має бути якась нова подія, зовсім несподівана, про яку ми не можемо здогадуватися, яка відведе нас ще далі від класичних ідей, але яка повністю змінить обговорення співвідношень невизначеностей. І коли цей новий розвиток подій відбудеться, люди вважатимуть досить марним те, що так багато дискутували про роль спостереження в теорії, бо тоді в них буде набагато ліпший кут зору, з якого можна дивитися на речі. Тож я скажу, що якщо ми зможемо знайти спосіб описати співвідношення невизначеностей та невизначеність сучасної квантової механіки, що відповідатиме нашим філософським ідеям, ми можемо вважати себе щасливчиками. Але якщо ми не зможемо знайти такого способу, це не повинно насправді турбувати. Ми просто повинні взяти до уваги, що перебуваємо на перехідному етапі, і що, мабуть, неможливо цілком отримати прийнятну картину для цього етапу.
Я позбувся труднощів 1 класу, сказавши, що вони насправді не такі важливі, що якщо комусь вдасться досягти прогресу з ними, то може вважати себе щасливчиком, а якщо ні, то це не повинно по-справжньому турбувати. Труднощі ж 2 класу справді серйозні. Вони виникають насамперед з того, що коли ми застосовуємо нашу квантову теорію до полів так, як маємо, якщо хочемо, щоб вона узгоджувалася зі спеціальною теорією відносності, інтерпретуючи її через тривимірні перерізи, про які я згадував, то отримуємо рівняння, які спочатку видаються добрими. Але коли спробувати їх розв’язати, виявляється, що в них немає ніяких розв’язків. Натепер ми повинні сказати, що в нас немає теорії. Але фізики дуже винахідливі щодо неї, і вони знайшли спосіб досягти прогресу всупереч цій перешкоді. Вони виявляють, що коли намагаються розв’язати рівняння, то складність у тому, що певні величини, які повинні бути скінченними, насправді нескінченні. Отримуються інтеграли, які розбігаються, замість того щоб збігатися до чогось визначеного. Фізики виявили, що існує спосіб давати раду цим нескінченностям за певними правилами, що дозволяє отримати визначені результати. Цей метод відомий як метод перенормування.
Я просто поясню ідею словами. Ми починаємо з теорії, що містить рівняння. У цих рівняннях трапляються певні параметри: заряд електрона, е, маса електрона, m, та інші подібного характеру. Потім виявляється, що ці величини, які з’являються у вихідних рівняннях, не рівні виміряним значенням заряду та масі електрона. Виміряні значення відрізняються від них певними поправковими членами – ∆e, ∆m тощо – так що загальний заряд дорівнює e + ∆e, а загальна маса – m + ∆m. Ці зміни заряду і маси відбуваються завдяки взаємодії нашої елементарної частинки з іншими речами. Тоді кажуть, що e + ∆e і m + ∆m, як спостережені речі, – важливі речі. Вихідні e і m – це просто математичні параметри; вони неспостережні, а отже просто засоби, які можна відкинути, коли вони надто далекі, щоб внести речі, які можна порівняти зі спостереженнями. Це був би цілком правильний спосіб продовжувати, якби ∆e та ∆m були малими (або навіть не такими маленькими, але скінченними) поправками. Однак, за фактичною теорією, ∆e і ∆m нескінченно великі. Попри цей факт, все ще можна використовувати формалізм і отримувати результати в термінах e + ∆e і m + ∆m, які можна інтерпретувати, сказавши, що вихідні e і m мають бути мінус нескінченність відповідної величини, щоб компенсувати нескінченно великі ∆e і ∆m. За допомогою теорії можна отримати результати, що можна порівняти з експериментом, зокрема що стосується електродинаміки. Дивно, що у разі електродинаміки отримуються результати, які надзвичайно добре узгоджуються з експериментом. Узгодженість стосується багатьох значущих цифр – така точність, що раніше була лише в астрономії. Саме завдяки цій хорошій узгодженості фізики надають певної цінності теорії перенормування, попри її нелогічний характер.
Здається, цілком неможливо поставити цю теорію на математично обґрунтовану основу. Свого часу фізична теорія була побудована на математиці, по суті підставовій. Я не кажу, що фізики завжди використовують підставову математику; вони часто використовують необґрунтовані кроки у своїх розрахунках. Але раніше, коли вони так робили, це було просто через, можна сказати, лінь. Вони хотіли отримати результати якомога швидше, не виконуючи зайвої роботи. Чистий математик завжди мав змогу прийти і зробити теорію обґрунтованою через подальші дії і, можливо, шляхом введення досить багатьох громіздких позначень та інших речей, бажаних з математичного погляду, щоб дістати все виражене строго, але zrf не робить внеску до фізичних уявлень. Раніша математика завжди могла так стати обґрунтованою, але з перенормуванням ми маємо теорію, що не піддається всім цим спробам математика зробити її підставовою. Я схильний вважати, що теорія перенормування – це те, що не збережеться в майбутньому, і що чудову узгодженість між її результатами та експериментом слід розглядати як випадковість.
Це, мабуть, не надто дивно, адже подібні випадки були в минулому. Справді, встановлено, що Борова теорія електронних орбіт дуже добре узгоджується зі спостереженнями, поки обмежуватися одноелектронними проблемами. Думаю, тепер люди скажуть, що ця узгодженість була випадковістю, бо основні ідеї орбітової теорії Бора були замінені чимось радикально відмінним. Я вірю, що успіхи теорії перенормування будуть на тій же основі, що й успіхи орбітової теорії Бора, застосованої до одноелектронних проблем.
Теорія перенормування усунула деякі з цих труднощів 2 класу, якщо можна прийняти нелогічний характер відкидання нескінченностей, але вона не усуває всіх. Залишилося чимало проблем щодо частинок, відмінних від тих, що входять в електродинаміку: нові частинки – мезони різного типу та нейтрино. Тут теорія все ще перебуває на примітивній стадії. Цілком певно, що доведеться кардинально змінити наші фундаментальні ідеї, перш ніж ці проблеми можна буде розв’язати.
Одна з проблем – та, про яку я вже згадував, стосується пояснення числа 137. Інші проблеми – як природним чином ввести фундаментальну довжину у фізику, як пояснити співвідношення мас елементарних частинок і як пояснити інші їхні властивості. Я вважаю, що для розв’язання цих окремих проблем будуть потрібні окремі ідеї, і що вони будуть розв’язуватися по черзі в ході послідовних етапів майбутньої еволюції фізики. Щодо цього я розходжуся з більшістю фізиків. Вони схильні думати, що буде виявлена одна головна ідея, яка разом розв’яже всі ці проблеми. Я думаю, що сподіватися, що хтось зможе розв’язати всі ці проблеми разом, – це вже занадто. Слід якомога більше відокремлювати їх одна від одної і намагатися розв’язувати окремо. І я вірю, що майбутній розвиток фізики полягатиме в розв’язанні їх по черзі, і що після розв’язання будь-якої з них все ще буде велика загадка, як приступати до наступних.
Певно, я міг би обговорити деякі свої ідеї щодо того, як підійти до деяких з цих проблем. Жодна з цих ідей не була глибоко розроблена, і я не надто сподіваюся на якусь із них. Але, думаю, що їх варто коротко згадати.
Одна з цих ідей – введення чогось, що відповідає світлоносному етерові, що був таким популярним серед фізиків ХІХ століття. Я вже говорив раніше, що фізика не еволюціонує назад. Коли я говорю про повторне введення етеру, то маю на увазі не повернення до картини етеру, що була в ХІХ столітті, а представлення нової картини етеру, яка відповідатиме нашим сучасним ідеям квантової теорії. Заперечення проти старої ідеї етеру полягало в тому, що якщо вважати, що це плин, який заповнює весь простір, то в будь-якому місці він має певну швидкість, що руйнує чотиривимірну симетрію, передбачену спеціальним принципом відносності Айнштайна. Спеціальна теорія відносності Айнштайна вбила цю ідею етеру.
Але, беручи до уваги нашу теперішню квантову теорію, нам більше не потрібно приписувати точну швидкість будь-якій певній фізичній речі, бо швидкість залежить від співвідношення невизначеностей. Що менша маса речі, яка нас цікавить, то важливіші співвідношення невизначеностей. Тепер, етер, безумовно, матиме дуже малу масу, тому співвідношення невизначеностей для нього будуть вкрай важливі. Отже, швидкість етеру в якомусь конкретному місці не слід подавати як точну, бо він буде суб’єктом співвідношення невизначеностей, і тому вона може бути яка завгодно в широкому діапазоні значень. Так можна подолати труднощі узгодження існування етеру зі спеціальною теорією відносності.
Це зробить одну важливу зміну в нашій картині вакууму. Ми хотіли б розглядати вакуум як зону, у якій маємо повну симетрію між чотирма вимірами просторочасу, як того вимагає спеціальна теорія відносності. Якщо є етер, що підпадає під співвідношення невизначеностей, неможливо буде мати цю симетрію точно. Можна припустити, що швидкість етеру з однаковою ймовірністю буде будь-якою в широкому діапазоні значень, що давало б симетричність лише приблизно. Ми не можемо якимось точним чином досягти межі враховування всіх значень швидкості між плюс і мінус швидкостями світла, що нам потрібно було б зробити, щоб симетрія стала точною. Отже, вакуум стає недосяжним станом. Я не думаю, що це фізичне заперечення проти теорії. Це означало б, що вакуум – стан, до якого ми можемо підійти дуже близько. Немає обмежень щодо того, як близько ми можемо підійти до нього, але ніколи не можемо його досягти. Я вважаю, що це було б цілком прийнятним для фізика-експериментатора. Однак означало б відступ від поняття вакууму, яке ми маємо в квантовій теорії, де ми починаємо з того, що вакуумний стан має саме ту симетрію, якої вимагає спеціальна теорія відносності.
Це одна ідея для розвитку фізики в майбутньому, яка змінила б наше уявлення про вакуум, але змінила б його таким способом, що не неприйнятний для фізика-експериментатора. Тут виявилося важко перейти до теорії, бо потрібно було б математично встановити співвідношення невизначеностей для цього етеру, а дотепер якась задовільна теорія в цьому напрямку не винайдена. Якби її можна було задовільно розробити, вона породила б новий вид поля у фізичній теорії, що може допомогти в поясненні деяких елементарних частинок.
Ще одна можлива картина, яку я хотів би згадати, стосується питання, чому всі електричні заряди, що спостерігаються в природі, повинні бути кратними одній елементарній одиниці, е. Чому немає неперервного розподілу заряду, що існує в природі? Картина, яку я пропоную, сходить до ідеї силових ліній Фарадея і передбачає розвиток цієї ідеї. Силові лінії Фарадея – це спосіб зображення електричних полів. Якщо ми маємо електричне поле в будь-якій області простору, то, за Фарадеєм, ми можемо провести набір ліній, що мають напрямок електричного поля. Близькість ліній одна до одної дає міру напруженості цього поля – вони близькі там, де поле сильне, і менш близькі – де слабке. Силові лінії Фарадея дають нам добру картину електричного поля в класичній теорії.
Коли ми переходимо до квантової теорії, то вносимо якийсь тип дискретності в нашу базову картину. Можна припустити, що безперервний розподіл силових ліній Фарадея, який ми маємо на класичній картині, замінюється лише кількома дискретними силовими лініями, між якими немає силових ліній. Тепер силові лінії на Фарадеєвій картині закінчуються там, де є заряди. Тому з цими квантованими силовими лініями Фарадея було б розумно припустити, що пов'язаний з кожною лінією заряд, який повинен лежати на кінці, якщо силова лінія має кінець, завжди однаковий (крім його знаку) і завжди є лише електронний заряд, - e або + e. Це приводить нас до картини дискретних силових ліній Фарадея, кожна з яких пов’язана із зарядом - e або + e. До кожної лінії прив’язаний напрямок, так що кінці лінії, що має два кінці, не однакові, а на одному кінці є заряд + e, а на другому – - e. Звісно, у нас можуть бути силові лінії, що тягнуться до нескінченності, і тоді заряду немає.
Якщо ми припустимо, що ці дискретні силові лінії Фарадея – щось базове у фізиці і лежать в основі нашої картини електромагнетного поля, nj дістанемо пояснення, чому заряди завжди виникають у кратних е. Бо якщо в нас є якась частинка, на якій закінчуються силові лінії, кількість цих ліній має бути цілим числом. Так ми отримуємо якісно цілком обґрунтовану картину.
Ми припускаємо, що ці силові лінії можуть переміщатися. Деякі з них, утворюючи замкнуті петлі або просто простягаючись від мінус нескінченності до нескінченності, відповідатимуть електромагнетним хвилям. Інші матимуть кінці, а кінцями цих ліній будуть заряди. Може бути, що силова лінія іноді розривається. Коли це трапляється, у нас з’являються два кінці, і на обох кінцях повинні бути заряди. Цей процес – розривання силової лінії – буде картиною створення електрона (e-) та позитрона (e+). Це була б цілком розумна картина, і якби хтось міг її розробити, це дало б теорію, у якій e з’являється як основна величина. Я ще не знайшов жодної розумної системи рівнянь руху для цих силових ліній, і тому просто висунув цю ідею як можливу фізичну картину, яку ми можемо мати в майбутньому.
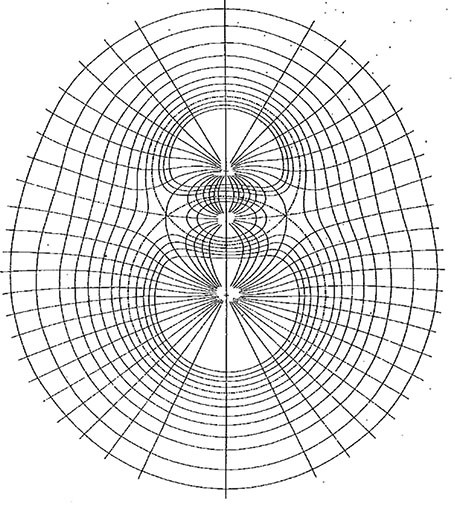
Силові лінії в електромагнетному полі, якщо їх вважати дискретними в квантовій теорії, вказують, чому електричні заряди завжди виникають як кратні зарядові електрона. На думку Дірака, коли силова лінія має два кінці, то на одному є частинка із зарядом - e, можливо, електрон, а на другому – частинка із зарядом + e, можливо, позитрон. Коли замкнена силова лінія розривається, виникає електрон-позитронна пара.
У цієї картини є одна дуже приваблива риса. Вона цілком змінить обговорення питань перенормування. Перенормування, яке ми маємо в нашій нинішній квантовій електродинаміці, починається з того, що люди називають голий електрон – електрон без заряду на ньому. На певному етапі теорії вносять заряд і накладають на електрон, завдяки чому останній взаємодіє з електромагнетним полем. Це приводить до збурення в рівняннях і спричиняє зміну маси електрона, ∆m, яку слід додати до попередньої маси електрона. Процедура швидше кружна, бо починається з нефізичної концепції голого електрона. Можливо, у покращеній фізичній картині, яку матимемо в майбутньому, голий електрон взагалі не існуватиме.
Такий стан справ – це саме те, що ми маємо з дискретними силовими лініями. Ми можемо зобразити силові лінії як струни, і тоді електрон на картині – кінець струни. Сама струна – це Кулонова сила навколо електрона. Голий електрон означає електрон без Кулонової сили навколо нього. Це немислимо з цією картиною, так само як немислимо думати про кінець шматка струни, не думаючи про саму струну. Це, гадаю, такий спосіб, яким нам слід спробувати розвинути свою фізичну картину – внести ідеї, які роблять немислимими речі, яких ми не хочемо мати. Знову ж таки, маємо картину, яка видається прийнятною, але я не знайшов належних рівнянь для її розвивання.
Я можу згадати третю картину, з якою маю справу останнім часом. Вона передбачає відхід від зображення електрона як точки і думання про нього як про своєрідну сферу кінцевого розміру. Звісно, це досить давня ідея зображати електрон як сферу, але раніше були труднощі з обговоренням сфери, що підлягає прискоренню та нерівномірному рухові. Вона буде викривлена, а як можна боротися з викривленнями? Я пропоную, що слід дозволити електронові мати загалом довільну форму і розмір. Будуть деякі форми та розміри, за яких він має меншу енергію, ніж за інших, і він прагнутиме набувати сферичної форми певного розміру, за якої електрон має найменшу енергію.
Ця картина розширеного електрона була простимульована відкриттям мю-мезона, або мюона, однієї з нових частинок фізики. Мюон має дивовижну властивість бути майже однаковим з електроном, за винятком однієї конкретної, а саме: його маса приблизно в 200 разів перевищує масу електрона. Окрім цієї різниці в масі, мюон надзвичайно схожий на електрон, маючи з надзвичайно високим ступенем точності той самий спін і той самий магнетний момент пропорційно до своєї маси, як і електрон. Це веде до припущення, що на мюон слід дивитись як на збуджений електрон. Якщо електрон – якась точка, уявляти, як він може збуджуватися, стає досить незручно. Але якщо електрон – найстабільніший стан для якогось об'єкта кінцевих розмірів, мюон може бути просто наступним найстабільнішим станом, за якого об'єкт зазнає свого роду коливань. Це ідея, над якою я працював нещодавно. У розвитку цієї ідеї виникають труднощі, зокрема труднощі з введенням правильного спіну.
Я згадав три можливі способи, якими можна подумати про розвиток нашої фізичної картини. Без сумніву, знайдуться й інші, про яких інші люди подумають. Хочеться сподіватися, що рано чи пізно хтось знайде ідею, яка справді підходить і веде до великого розвитку. Я досить песимістичний щодо цього і схильний думати, що жодна з них не буде достатньо хороша. Майбутня еволюція базової фізики – тобто розвиток, який дійсно розв’яже одну з фундаментальних проблем, таких як внесення фундаментальної довжини або обчислення співвідношення мас – може вимагати набагато різкіших змін у нашій фізичній картині. Це означало б, що в наших теперішніх спробах продумати нову фізичну картину ми налаштовуємо свою уяву на роботу в термінах неадекватних фізичних концепцій. Якщо це справді так, як ми можемо сподіватися на прогрес у майбутньому?
Є ще одна лінія, якою можна далі рухатися теоретичними засобами. Видається, одна з фундаментальних особливостей природи – те, що фундаментальні фізичні закони описуються в термінах математичної теорії великої краси та сили, вимагаючи досить високого рівня математики для її розуміння. Ви можете здивуватися: чому природа побудована саме за таким принципом? Можна лише відповісти, що наші сучасні знання, видається, свідчать, що природа побудована nfr. Ми просто повинні це прийняти. Можна описати ситуацію, сказавши, що Бог – математик дуже високого рівня, і Він використовував дуже розвинуту математику при побудові Всесвіту. Наші слабкі математичні спроби дають нам змогу зрозуміти якийсь шматок Всесвіту, і, в міру того як ми продовжуємо розвивати дедалі вищу математику, можемо сподіватися зрозуміти Всесвіт краще.
Цей погляд забезпечує нам інакший спосіб, яким ми можемо сподіватися досягти успіхів у своїх теоріях. Просто вивчаючи математику, ми можемо сподіватися здогадатися про тип математики, який увійде у фізику майбутнього. Багато людей працюють над математичними засадами квантової теорії, намагаючись краще зрозуміти теорію та зробити її потужнішою та красивішою. Якщо хтось зможе знайти правильні лінії, за якими можна досягти такого розвитку, це може привести до майбутнього прогресу, коли люди спочатку виявлять рівняння, а потім, перевіривши їх, поступово навчаться застосовувати. Певною мірою це відповідає лінії розвитку, що сталася з Шредінґеровим винайденням хвильового рівняння. Шредінґер виявив його, просто шукаючи рівняння математично красиве. Коли рівняння було вперше виявлене, люди побачили, що воно придатне певним чином, але загальні принципи, згідно з якими його слід застосовувати, були розроблені лише через два-три роки. Цілком може бути, що наступний прогрес у фізиці відбудеться в такому напрямку: люди спочатку виявляють рівняння, а потім потрібні будуть кілька років розвитку, щоб знайти за рівняннями фізичні ідеї. Я вважаю, що це швидше лінія прогресу, ніж спроба вгадати фізичні картини.
Звісно, може бути, що навіть ця лінія прогресу зазнає невдачі, і тоді залишиться лише експериментальна. Фізики-експериментатори продовжують свою роботу абсолютно незалежно від теорії, збираючи величезну скарбницю інформації. Рано чи пізно з’явиться новий Гайзенберґ, який зможе виділити важливі особливості цієї інформації і побачити, як використовувати їх способом, подібним до того, яким Гайзенберґ використовував експериментальні знання про спектри для побудови своєї матричної механіки. Цілком можливо, що фізика врешті розвиватиметься за цими лініями, але нам, можливо, доведеться чекати досить довго, якщо люди не запропонують яскравих ідей для розвитку теоретичної сторони.